High Power Amplifier in Multi-tone environment

A multi-tone signal can be characterized by the average and the peak power. The average power is defined as a sum of the power value of each of the tones. For example, if we have 4 tones at +5dBm each, the average power would be:

+5 dBm + 6 = +11 dBm.

The peak power, otherwise known as peak envelope power (PEP), is the maximum instantaneous power of the combination of the all tones. If each tone has power P1, the amplitude of the voltage of each tone is V1= √ 2*P1*R, where R is the load value, typically 50 ohms. Maximum peak voltage on the load happens at the moments of time when all the voltage vectors from each of the independent tones are aligned. At this moment, the total amplitude of voltage across the load is V_peak=V1*N, where N is the number of independent tones. Therefore, the peak power is equal to:

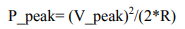
or

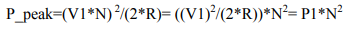
The following table gives the average and peak power for multi-tone signal (in mW), assuming that all the tones are independent and equal in power level (1 mW each).

The following table gives the average and peak power for multi-tone signal (in dBm), assuming that all the tones are independent and equal in power level (0dBm each).

For example, if we have 9 tones with -2 dBm of each tone, the peak power would be 81 times or 19.1 dB more than single tone:

P_peak= -2dBm+19.1=+17.1dBm

At the same time the average power would be only 9.5 dB higher than the power level of each tone. Therefore, the peak power is 9.6dB more than the average power for this particular example. If we have an amplifier with a certain output power, 100W for example, and we would like to have "low" distortions, then we have to limit the input power of the multi-tone signal so that the peak power on the output of the amplifier is equal to 100W. In case of N=9 tones, each tone on the output would be 100(W)/81= 1.2W, or +30.9dBm. If the low drive gain of that amplifier is 50dB, the input power of each tone should be:

+30.9 dBm - 50 = -19.1 dBm.

If higher distortions is acceptable, the level of each tone could be higher, to a maximum of 1/9 of the total output power. So, each tone on the output would be 100(W)/9= 11W, or +40.5dBm. If the high drive gain of that amplifier is 47dB (50dB-3dB compression), the input power of each tone should be:

+40.5 dBm - 47 = -6.5 dBm.

If much greater power level of each tone is applied to the input of the amplifier (for example -2 to -1dBm), it drives the amplifier to deeper RF overload creating more stress and does not produce any more RF power on the output. The level of input power of each tone of the multi-tone signal should be set by taking into consideration the number of tones and desired level of distortion.